
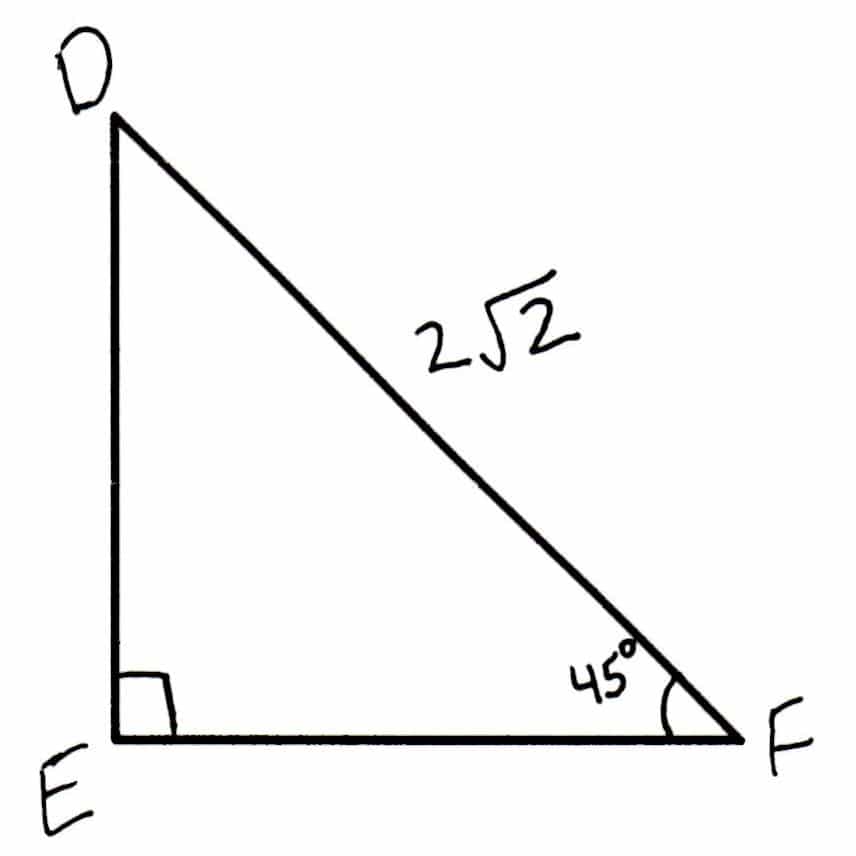
They are worth practicing, especially because triangles are the GMAT’s favorite plane geometry shape! We’ll see them in both Problem Solving and Data Sufficiency. Remember your special right triangle ratios. If you chose (B), this tells us we’re dealing with special right triangles, but without a value for at least one side, we can’t tell if the area will be less than 5 because we can’t find the area. Remember, we can’t estimate, or “eyeball” the figure. If you chose (A), this gives us a value for one side, but we still can’t determine whether the area is greater than 5 for the entire figure without more information. Since ?3 is more than 1, we know the total area will be more than 5. Now we can see the height is 2, and the base is 2+2?3. Remember the special right triangles ratios! But since it’s a “yes or no” question, we’ll want to solve for the area to see whether it is less than 5. If this was a “value” question, we’d be done and not have to actually solve. Since we’re dealing with special right triangles, we already know we will be able to move information from one part of the triangle to the other and eventually find the area.

If we choose AC as our base, we’ll need to draw an altitude to create a height.Īt a minimum, we’ll probably need to use BOTH pieces of information given in the statements to try and find both the length of our height AND our base, so let’s fill that information in: Some of the worksheets for this concept are find the missing side leave your answers as, properties of right triangles, infinite geometry, special right triangles, infinite geometry, a b solving 306090 c solving 454590, dn on back of packet name per lo i can prove the, infinite geometry. We know the formula for the area of a triangle is (1/2)(B)(H). It’s important to always draw figures that are described but not provided: In triangle ABC, angle ABC is 105 degrees. Don’t confuse it with the 45-45-90 ratio, and think that the x?3 should be on the hypotenuse! Let’s check out a sample Veritas Prep question: Remember that for the 30-60-90 triangle, the hypotenuse (longest side) is the side that has the ratio of 2x. Its sides will always be in a ratio of x: x: x?2.
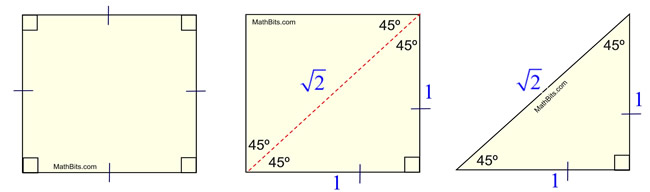
The other special triangle is the 45-45-90 triangle. Its sides will always be in a ratio of x: x?3 : 2x. If we know the value of one side, we can find the values of all the other sides. The special right triangles are so called because their side-ratio never changes. Geometry is essential to GMAT Quantitative success, and knowing the special right triangles are a fundamental “you-will-definitely-see-it” type of concept. The proportion of the lengths of the sides are x: x √ 3: 2x.Vivian Kerr is a regular contributor to several GMAT and SAT websites, allowing her to flex her intellectual muscle while she is in between film and stage project as an actress. This is a special angle triangle whose angles are 30 ° 60 ° 90 °. + x2= 2×2 Locate the square root of each term in the formula √ x2 + √ x2 = √( 2×2).įor that reason, the hypotenuse of a 45 ° 45 ° 90 ° triangle is x √ An isosceles triangle is a triangle in which two the lengths of its two sides are equal, and likewise, both of its angles are equal.īy utilizing the formula of a special right triangle a2 + b2 = c2, we can determine the hypotenuse of a 45 ° 45 ° 90 ° triangle as complies with: Because a 45 ° 45 ° 90 ° triangle is additionally an isosceles triangle let a Now, you can see – Base: Height: Hypotenuse = x: x: x √ 2 = 1: 1: √ 2.Īlternatively, a 45 ° 45 ° 90 ° triangle can additionally be an isosceles triangle. The proportion of the base to height to this triangle’s hypotenuse is 1: 1: √ 2. In particular, the right triangle angles are 45 °, 45 °, and also 90 °. Let’s have a short introduction of these special right triangles as we will see them thoroughly in the next articles. By utilizing the Pythagorean Thesis, discovering the absent side of a triangle is relatively easy and straightforward. In geometry, the Pythagorean Theory is a declaration that shows the partnership of the sides of the best triangle.Ī right triangle formula is provided by a2 + b2 = c2, where either b or a is the triangle’s base and height. Special right triangles are triangles whose sides remain in a particular proportion, referred to as Pythagorean Triples.


 0 kommentar(er)
0 kommentar(er)
